03.12.2013
تأخذ المتباينة الخطية فى متغيرين الصورة العامة الآتية :
أ س + ب ص + جـ > صفر
حيث : أ ، ب ، جـ أعداد حقيقية ، أ ، ب ≠ صفر معا .
وكما سبق بالنسبة للصورة العامة للمتباينة الخطية فى متغير واحد فإن علامة
التباين (>) يمكن أن تستبدل بإحدى العلامات ( ≤) أو (<) أو (≥ ).
حل المتباينة الخطية في متغيرين
هو مجموعة الازواج المرتبة التي تحقق المتباينة اي تجعلها صحيحة
و لحل المتباينة الخطية بمتغيرين نتبع الخطوات الآتية :-
1) نكتب المتباينة على صورة معادلة خطية بمتغيرين
2) نمثل المعادلة الخطية بيانيا في المستوى الديكارتي بطريقة المقطعين او بطريقة الجداول و ذلك بجعل ص موضوعا للقانون ثم تكوين جدولا مناسبا بقيم س و قيم ص المناظرة لها
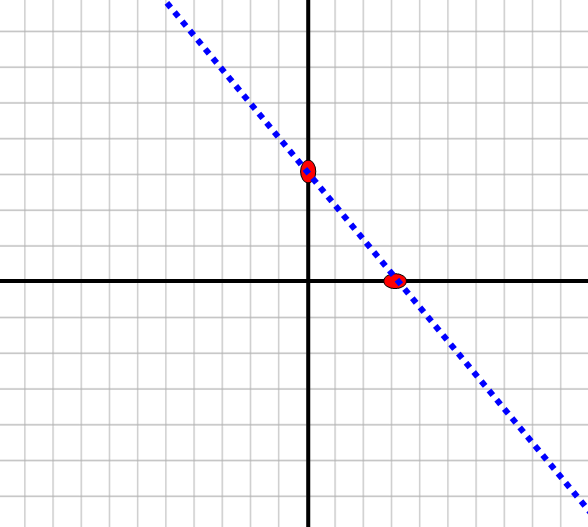
3) اذا كانت المتباينة التي نريد حلها تحتوي اشارة مساواة نرسم خطا متصلا اما اذا كانت المتباينة لا تحتوي اشارة مساواة فنرسم الخط متقطعا
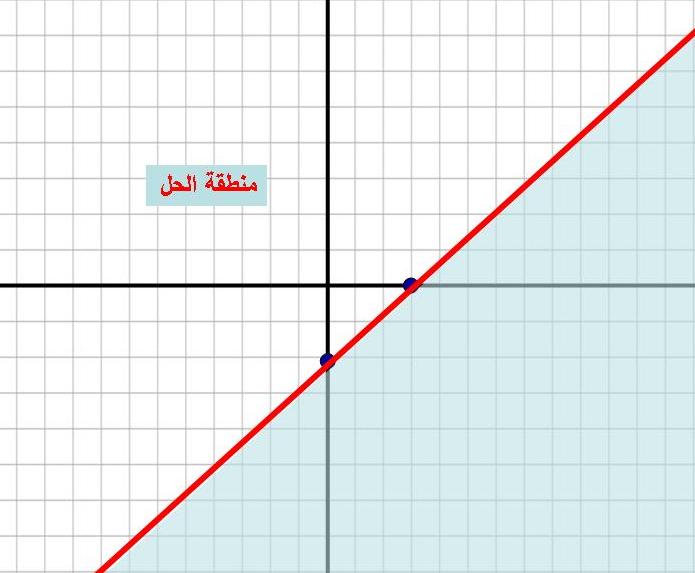
4) بعد رسم الخط المستقيم سنلاحظ أنه يقسم المستوى الديكارتي إلى منطقتين احداهما هي منطقة الحل و الأخرى هي منطقة عدم الحل و لتحديد اي منهما هي منطقة الحل نقوم باختيار نقطة من إحدى المنطقتين و اختبار ما اذا كانت تحقق المتباينة
فاذا كانت النقطة المختارة تحقق المتباينة فهي في منطقة الحل و اذا لم تحقق المتباينة فهي في منطقة عدم الحل
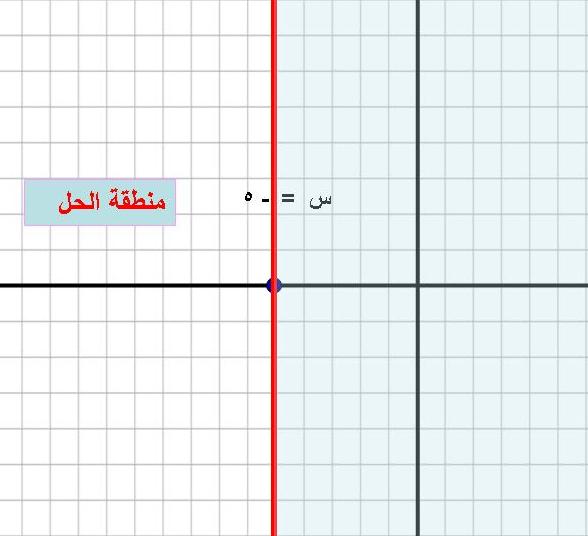
5) نكتب على المنطقة التي تحقق المتباينة " منطقة الحل " و نظلل منطقة عدم الحل
عدل سابقا من قبل رانية شريم في الثلاثاء 3 ديسمبر - 22:56 عدل 1 مرات